Бущан Григорий.
Накопилось множество наблюдательных материалов, чтобы с достаточной степенью достоверности утверждать, что, при некоторых условиях, макротела ведут себя в гравитационном поле, подчиняясь квантовым законам. К одному из таких эффектов можно отнести и эфект Джанибекова породивший столько дискуссий в связи с предполагаемой опасностью, суть которой состоит в том, что Земля может совершить кувырок на 180 градусов.
Накопилось множество наблюдательных материалов, чтобы с достаточной степенью достоверности утверждать, что, при некоторых условиях, макротела ведут себя в гравитационном поле, подчиняясь квантовым законам. К одному из таких эффектов можно отнести и эфект Джанибекова породивший столько дискуссий в связи с предполагаемой опасностью, суть которой состоит в том, что Земля может совершить кувырок на 180 градусов.
После краткого введения, перейдем к сути вопроса и попробуем пояснить, как эффект Джанибекова может быть связан с квантовой механикой.
Все знают квантовомеханическое уравнение Шредингера.
![i\hbar\frac{\partial}{\partial t} \Psi(\vec{r} ,t) = \left [ -\frac{\hbar^2}{2m}\nabla^2 + V(\vec{r},t)\right ] \Psi(\vec{r} ,t)](http://upload.wikimedia.org/math/2/d/4/2d4f51c0eaecc66dbfb18fc887f711de.png)
В этом уравнении присутствует постоянная Планка - очень маленькая величина, чтобы проявить себя на макроуровне.
Сделаем первое предположение - постоянная Планка есть постоянная, которая, хоть и имеет механическую размерность, но, возможно не является единственной константой описывающей все механические процессы, а проявляет себя только на микроуровне, а для описания гравитационно - инерциальных процессов на макроуровне возможно существует иная постоянная, размерность и физический смысл которой еще предстоит разгадать.
Итак, эффект Джанибекова состоит в том, что пролетев некоторое расстояние рогами вперед, гайка вдруг делает кувырок и летит рогами назад.
Для классического движения это не характерно. Просто нет энергии для кувырка, чтобы из состояния А перейти в состояние В.
Другое дело квантовый объект, который находится в потенциальной яме в состоянии А ( рогами вперед). Такой объект, может, при помощи туннельного эффекта перейти в состояние В и затем, с определенной вероятностью, снова перейти в состояние А.
Для наглядности вспомним теорию туннельного эффекта.
При прочтении, нижеследующего текста, надо помнить о следующих аналогиях. Итак, чтобы перейти из состояния А в состояние В гайке нужно совершить боковой кувырок. То есть энергия бокового кувырка Е2 плюс энергия основного вращения Е1 и будет считаться высотой потенциального барьера.
Согласно классической механике, частица может находиться лишь в тех точках пространства, в которых её потенциальная энергия — Upot, меньше полной. Это следует из того обстоятельства, что кинетическая энергия частицы
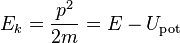 не может (в классич. физике) быть отрицательной, так как в таком случае импульс будет мнимой величиной. То есть, если две области пространства разделены потенциальным барьером, таким, что
не может (в классич. физике) быть отрицательной, так как в таком случае импульс будет мнимой величиной. То есть, если две области пространства разделены потенциальным барьером, таким, что  ,
просачивание частицы сквозь него в рамках классической теории
оказывается невозможным. В квантовой же механике мнимое значение
импульса частицы соответствует экспоненциальной зависимости волновой
функции от её координаты. Это показывает уравнение Шрёдингера с постоянным потенциалом:
,
просачивание частицы сквозь него в рамках классической теории
оказывается невозможным. В квантовой же механике мнимое значение
импульса частицы соответствует экспоненциальной зависимости волновой
функции от её координаты. Это показывает уравнение Шрёдингера с постоянным потенциалом:
(упрощенное уравнение Шрёдингера в одномерном случае)
где
 координата;
координата;  полная энергия,
полная энергия,  потенциальная энергия,
потенциальная энергия,  редуцированная постоянная Планка,
редуцированная постоянная Планка, 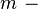 масса частицы).
масса частицы).- Если
 , то решением этого уравнения является функция:
, то решением этого уравнения является функция:

 , а потенциал частицы до и после барьера
, а потенциал частицы до и после барьера  . Пусть также начало барьера совпадает с началом координат, а его «ширина» равна
. Пусть также начало барьера совпадает с началом координат, а его «ширина» равна  .
.Для областей
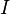 (до прохождения),
(до прохождения),  (во время прохождения внутри потенциального барьера) и
(во время прохождения внутри потенциального барьера) и  (после прохождения барьера).получаются соответственно функции:
(после прохождения барьера).получаются соответственно функции:


где
 ,
, 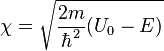
Так как слагаемое
 характеризует отраженную волну, идущую из бесконечности, которая в данном случае отсутствует, нужно положить
характеризует отраженную волну, идущую из бесконечности, которая в данном случае отсутствует, нужно положить 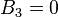 .
Для характеристики величины туннельного эффекта вводится коэффициент
прозрачности барьера, равный модулю отношения плотности потока прошедших
частиц к плотности потока упавших:
.
Для характеристики величины туннельного эффекта вводится коэффициент
прозрачности барьера, равный модулю отношения плотности потока прошедших
частиц к плотности потока упавших:
Для определения потока частиц используется следующая формула:

где знак * обозначает комплексное сопряжение.
Подставляя в эту формулу волновые функции, указанные выше, получим

Теперь, воспользовавшись граничными условиями, выразим сначала
 и
и  через
через  (с учетом, что
(с учетом, что  ):
):

а затем
 через
через  :
:
Введем величину
 о
окоторая будет порядка единицы. Тогда:

Получена экспоненциальная формула для определения коэффициента прозрачности барьера, которая показывает какой процент частиц преодолеет потенциальный барьер. Надо отметить, что мы не ставим перед собой задачу решить количественно проблему эффекта - это задача очень сложная. К тому же мы не знаем чем заменить постоянную Планка - не знаем ни размерности ни значения новой константы и даже не можем определить, что в нашем случае будет шириной потенциального барьера а. Можно только сказать, что поскольку высота потенциального барьера в нашем случае Е1 + Е2, тоU0 можно заменить этой суммой, а полная энергия системы Е равна, в нашем случае, Е1.
Таким образом U0 - E будет равно Е1 + Е2 - Е1 = Е2, то есть равна энергии бокового кувырка.
Чтобы доказать квантовую природу эффекта Джанибекова, надо две абсолютно идентичные гайки закрутить с максимально возможно одинаковой скоростью вращения, чтобы можно было считать эти гайки пребывающими в коллективном квантовом состоянии.
Если объекты будут находиться в коллективном состоянии их квантовое взаимовлияние сразу же проявит себя.
Это не единственное явление в космосе, которое проявляет себя как квантовое.
Перечислю некоторые из них.
1) Поведение третьей ступени ракеты выводящей спутник на орбиту, когда она, перейдя на более низкую орбиту обгоняет спутник.
2) Спускаемый аппарат, входя в плотные слои атмосферы, ускоряется, вместо того чтобы тормозиться.
3) Неоторые спутники Сатурна обладают удивительной особенностью - они периодически "обмениваются" своими орбитами. Например, Янус и Эпиметей (с которым едва не столкнулся зонд "Пионер-11"), двигаясь по очень близким орбитам, постепенно сближаются. В результате взаимного притяжения движение внутреннего спутника ускоряется, и он переходит на более высокую орбиту, а внешний замедляет свой бег и занимает место внутреннего. Такой "обмен" происходит у них каждые три года. Кроме них, существует еще одна такая "коорбитальная пара" Диона - Елена и "трио" Тефия - Телесто - Калипсо. Причем, интересно отметить, что спутники Янус и Эпиметей в четыре раза различаются по массам, и они не слипаются на какой- нибудь усредненной орбите, а словно электроны обмениваются орбитами.
Еще одним подтверждением того, что макротела в ближнем космосе ведут себя, как элементы квантовой системы, является движение астероида Тутатиса или Таутатиса, который периодически сближается с Землей и, который имеет то ли две, то ли три собственные оси вращения.
Для классического объекта это невозможно, но для элемента квантовой системы - вполне. Это,тот же эффект Джанибекова, только гайка Джанибекова имеет только две разрешенные оси вращения, а Тутатис имеет несколько, а две или три из них являются наиболее вероятными. Количество осей, по видимому, зависит от массы объекта.
_%D0%A2%D0%B0%D1%83%D1%82%D0%B0%D1%82%D0%B8%D1%81.jpg)